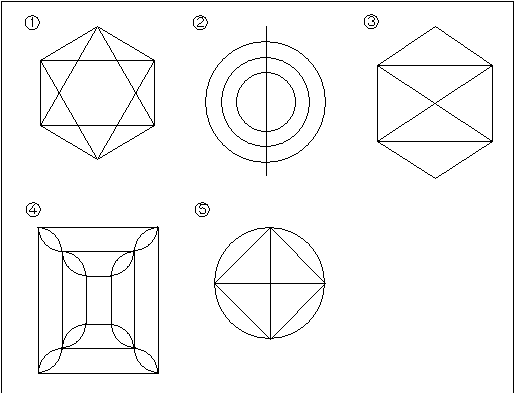
<問題>
下の①~⑤のうちで、一筆書きができないものを選んで記号で答えなさい。(01年多摩大目黒)

入試問題に挑戦第13回解答編
<解答>
一筆書きの問題は、『ケーニヒスベルクの7つの橋』の問題が不可能であることをオイラーが証明したことで、有名です。どんな問題であるのかは、ここでは省略させて頂きますが、一筆書きができる図形と、できない図形を簡単に見分けるには、このオイラーの考え方を利用します。
まず、図形の頂点や線の交点などに注目して、その点から出ている線が何本あるのかで、点を分類します。点から出ている線の本数が奇数本のときを奇数点、線の本数が偶数本のときを偶数点と呼ぶことにします。
問題の図形に、奇数点、偶数点を記入すると、以下の様になります。
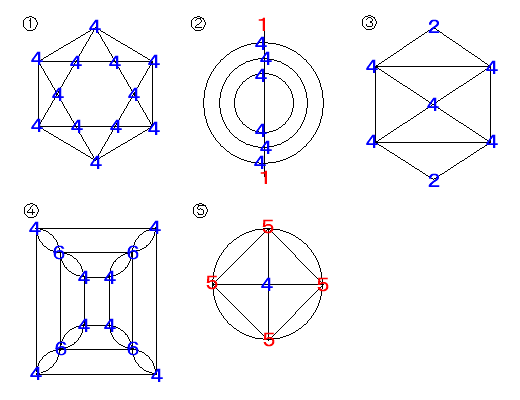
ここで、奇数点と偶数点の違いについて考えてみましょう。一筆書きで点を通過する場合には、その点に入る線と出る線が必要です。つまり線が2本あれば点を通過できますから、点から出ている線の本数が2の倍数(偶数)本の時には、その点を通過点と考えることが出来ます。
ところが、点から出ている本数が奇数本の時は、1本半端が出てしまいます。その半端の1本から入った場合は、その点から出ることができないので、通過点とはなりません。そこで、この奇数本の点を、始点、または終点と考えればよいことになります。
ただし、一筆書きという条件ですから、始点、終点は各1個ずつしかとれません。つまり、奇数点が3個以上ある場合には一筆書きができないということになります。
また、線は点どうしを結んでいるので、線1本につき、その両端の点で各1本ずつ2回本数を数えていることになるので、各点の本数の合計は必ず2の倍数(偶数)になります。従って、奇数点の個数は、必ず0または、偶数個になることがわかります。
以上のことをまとめてみると、
①奇数点が0個(すべて偶数点)の場合は、どの点からはじめても一筆書きが可能。
②奇数点が2個の場合は、一方の奇数点を始点、他方を終点とすることで一筆書きが可能。
③奇数点が2個より多い場合は、一筆書きが不可能。
これより、問題の答えは【⑤】になります。