入試問題に挑戦第４回
　またまた、図形問題です。中学入試では何度も登場してきた問題ですが、あえて麻布が今年出題してきたのには、どの様な意図が隠されているのでしょうか。もしかすると、２００２年問題への布石かも・・・。

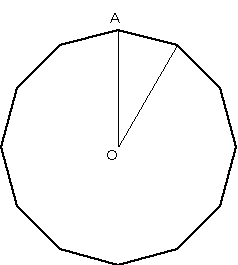
　下の図は正１２角形で、点Ｏはその中心です。次のように１つの頂点をＡとするとき、ＯＡの長さは１ｃｍです。この正１２角形の面積を求めなさい。（０１年麻布）

入試問題に挑戦第４回・解答編

　この問題は５年生分野で、多角形の性質をきちんと理解し、また３０度を活用できたかどうかがポイントです。基本的な知識を整理できているかどうかを確認する問題として、これまで多くの学校で出題されたことがあります。

　まず、正１２角形の中心Ｏから各頂点へ直線を引くと合同な二等辺三角形１２個に分けられますから、二等辺三角形１個分の面積を求めて１２倍すればよいことになります。

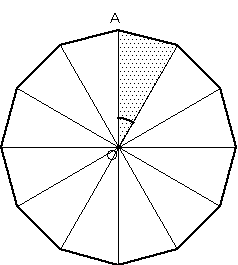
　この二等辺三角形は頂角が、３６０÷１２＝３０（度）なので、１ｃｍの辺を底辺として下の図のように見たときの高さ（点線ＡＢ）がわかれば、面積が求められます。

　ここで、三角形ＯＡＢに注目すると、角度が３０度・６０度・９０度の直角三角形になっています。この三角形は中学入試では頻出の三角形であり、三角定規の１つとしても有名です。この三角形は正三角形の半分なので、ＡＢの長さはＯＡの長さの半分になります。

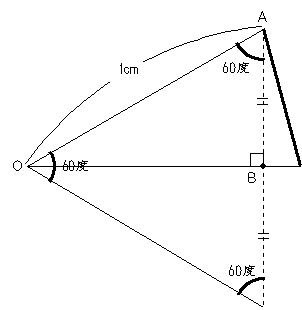
　三角形ＯＡＢ＝１×０．５÷２＝０．２５（平方ｃｍ）

　以上から、正十二角形の面積は、０．２５×１２＝３（平方ｃｍ）になります。

　ここで少し余談ですが、この正十二角形に半径１ｃｍの円を重ねてみます。すると円と正十二角形の間に隙間ができ、この部分の面積を求める問題が、中学入試の出題されたこともあります。実際に計算してみると、１×１×３．１４−３＝０．１４（平方ｃｍ）です。

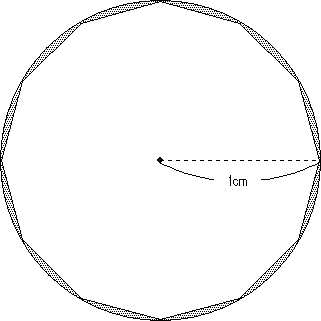
　ところが、２００２年からの新学習指導要領によれば、円周率は「３」を使うことになります。すると、先の隙間の部分の面積は、１×１×３−３＝０。なんと、面積が「０」です。つまり、円と正十二角形は面積が等しいということになってしまうのです。本当にこれでいいんでしょうか？

　今年の麻布が、使い古された問題をあえて出題してきたのは、もしかしたら、２００２年の指導要領への密かな警鐘なのかもしれません。